Lies, damned lies, and rankings: the problem with Bloomberg's COVID resilience ranking
Every ranking creates winners and losers. In the case of Bloomberg’s Covid Resilience Ranking, the Philippines is a loser: dead last and called the worst place to be during the pandemic. A damning judgment that the country’s vaccine czar, Carlito Galvez, Jr., says isn’t fair due to a biased scoring methodology. Is Bloomberg’s ranking biased, or is this just a sore loser making excuses?
The illusion of objectivity
When faced with a complex world, scores and rankings offer an irresistible simplification to seemingly intractable questions. Bloomberg’s Covid Resilience Ranking attempts to distill how well a country is handling the pandemic with the “least amount of social and economic upheaval” into a single number. This score consolidates at least 12 different factors that span three broader categories: COVID status, re-opening progress, and quality of life.
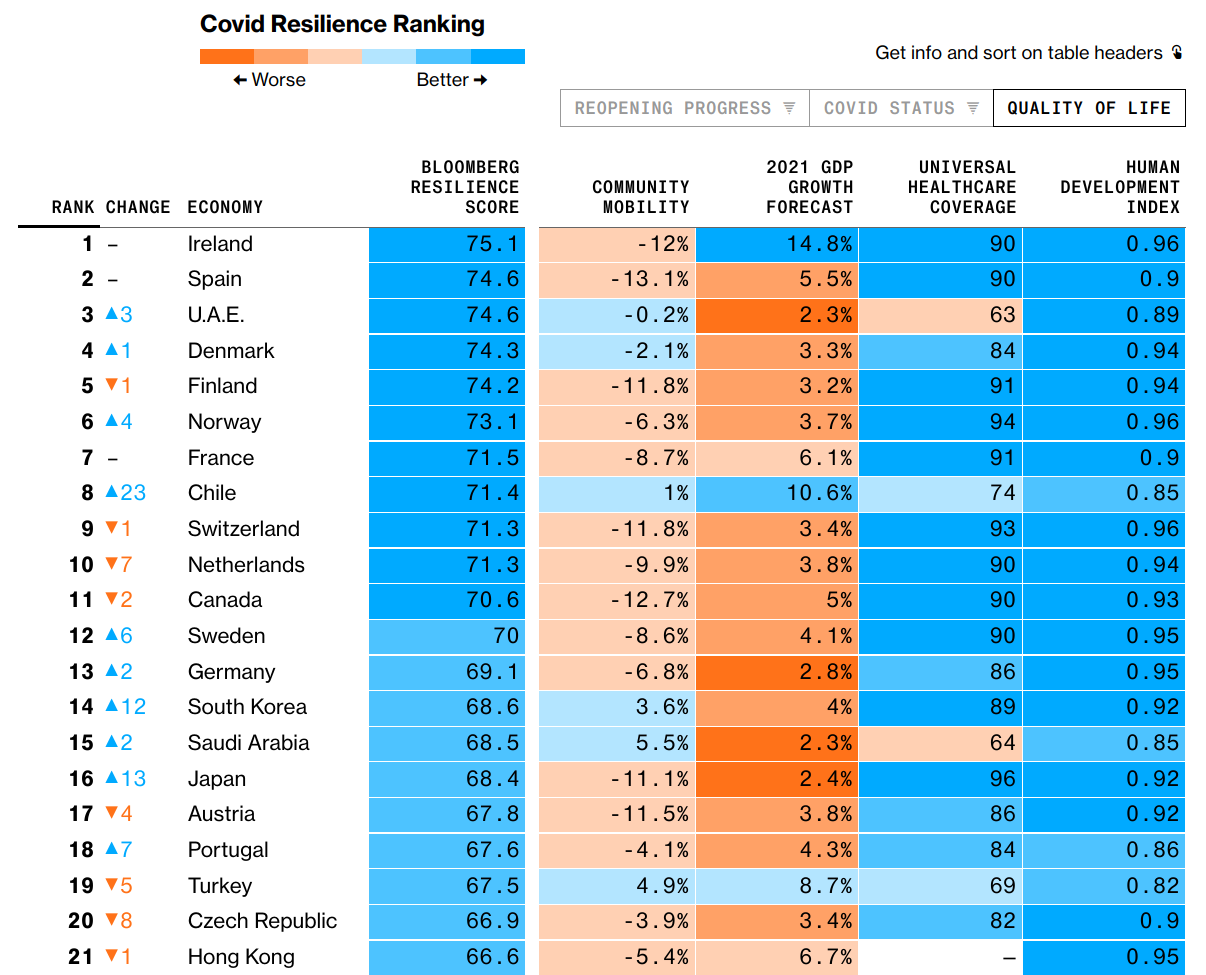
On the surface this resilience score is objective since each factor is quantitative and some underlying mathematical formula is used to define the score. Unfortunately, the use of mathematics and algorithms doesn’t guarantee objectivity. Every scoring system hides bias within its nooks and crannies. Some common sources of bias include:
- the choice of data, which often manifests as selection bias,
- the choice of factors, which is part of the design process, and
- the choice of weights, which is also part of the design of the score.
In terms of data, what are included is just as important as what are omitted. Galvez argues that only 53 countries are included when there are 203 nations globally. This sort of selection bias may not necessarily affect the score, but it could result in the Philippines leaving behind the ignomy of being the worst country to be in for COVID.
The choice of factors in a score is inherently biased, since it is a design process. Someone must decide which factors to include and why. Even in predictive models, the choice of factors can be biased. Someone p-hacking results or prey to confirmation bias will choose specific features to get a result they want, leading to a biased model.
Galvez argues that the resilience ranking overly emphasizes economics and underweights health outcomes. If additional health factors were added, such as oxygen supply, the Philippines could have a higher score and potentially move out of last place. But crying foul of bias while attempting to assert your own seems disingenuous at best.
In addition to the choice of factors, the weights used for each factor are also biased. In scoring models, weights quantify our perception of importance. A weighted average or equally weighted score imply every factor has equal importance. Other scores may have different weights that prioritize some factors over others. For example, job candidates might be evaluated on a nunber of criteria, including GPA. This may not be super important and therefore be underweighted relative to other factors, such as years of experience.
A financial news provider like Bloomberg may arguably overweight economic factors over other factors. Whether or not that’s fair is in the eye of the beholder. Either way, we don’t really know, since Bloomberg only publishes the factors included and not their weights or methodology.
Using regression to reverse engineer a score
The central argument in Galvez’s rebuttal is that a different set of factors would be more fair and that the Philippines wouldn’t be last if that were the case. If we knew Bloomberg’s approach to their COVID resilience ranking, we could easily twst whether this argument is valid or not.
Despite an opaque methodology, we can reconstruct Bloomberg’s scoring formula with a linear regression. Many scores are simply a weighted sum (or weighted average) of a set of factors:
$ score = w_1 x_1 + w_2 x_2 + … + w_n x_n + C $
Notice that this formulation is the same as a linear regression, so the fit should be extremely good and have small residuals.
model <- lm(score ~ ., df)
Indeed, the model has an $R^2$ of 99.99% with all p-values less than $2^{-16}$.
The model gives us the weights for each of the 12 factors plus an intercept term, which scales the score between 1 and 100.
Coefficients:
(Intercept) pct.vax lockdown.severity flight.capacity
3.484e+01 8.792e+00 -1.328e-01 8.837e+00
travel.routes.vax X1m.cases X3m.fatality total.deaths
3.201e-02 -4.240e-03 -1.083e+02 -1.362e-03
positivity.rate mobility gdp.forecast universal.health
-3.704e+01 9.985e+00 5.916e+01 1.453e-01
hdi
1.966e+01
In a standard analysis we would try to reduce the number of features in the model based on weight of evidence or variable importance. In this case we are reverse engineering a score with a fixed set of known variables. So rather than identify the variables driving a response we want to know what the score looks like if we drop some features or change their weights given a baseline.
Complaining doesn’t make it better
Now that we have a model for COVID resilience, let’s revisit Galvez’s claims. The first rebuttal was that only 53 out of 200 countries were included, so Philippines shouldn’t be considered worst. Fair point, but in terms of the resilience score, the Philippines is well below the median of 65.3 and the top scorers are at least 75% better. So arguing “we’re not last” is lipstick on a pig.
In terms of overemphasis on economic factors, let’s remember Bloomberg operates in the financial industry. It would be out of character if they didn’t emphasize financial factors. That said, given our model, let’s remove GDP growth forecast and see whether it affects the ranking:
> score <- get_score(m1,df, 'gdp.forecast')
> score[order(score, decreasing=TRUE)]
U.A.E. Denmark Finland Spain Norway
73.28225 72.33159 72.28232 71.32348 70.92384
Switzerland Netherlands France Canada Sweden
69.36579 68.85232 67.79690 67.75746 67.61915
Germany Saudi Arabia Japan Ireland South Korea
67.58230 67.13115 66.98451 66.35466 66.30705
Austria Portugal Chile Czech Republic Belgium
65.55060 65.08572 65.04787 64.84809 63.26805
Turkey Italy U.S. Greece U.K.
62.30962 62.18414 61.96232 61.76198 61.45785
Colombia Mainland China Australia Israel New Zealand
60.79171 60.32333 59.86179 59.29019 58.25961
Poland Bangladesh Pakistan Iraq South Africa
58.00616 56.70804 56.33100 55.09957 54.76407
Nigeria Mexico Singapore Argentina Russia
54.69437 53.88603 53.62846 53.13737 52.21596
India Taiwan Peru Indonesia Malaysia
50.30832 50.16986 50.12612 48.33467 46.58546
Thailand Romania Vietnam Philippines Hong Kong
46.36560 45.35464 41.06285 37.92085 NA
Brazil Iran Egypt
NA NA NA
Nope, the Philippines is still last.
We can continue this game until we hit a set of features where the Philippines is not last. However, in a nunber of permutations I tried, the Philippines was still in the bottom X. I’ll leave it as an exercise of the reader to exhaustively evaluate all combinations of factors.
The myth of COVID resilience
Despite the poor showing of the Philippines, Galvez has a point: scores and rankings are biased. Scores appear to be objective, but the reality is that the very act of defining the score introduces bias. This is how standardized tests like the SAT inadvertently penalize poor kids and how facial recognition systems can’t recognize black people.
In the case of COVID resiliency, COVID severity is highly localized. In the United States, resiliency depends on the state you live in. One single number just can’t do justice. The same is true in the Philippines, where the NCR (national capital region) may be in a totally different situation than the rest of the country.
Despite embedded bias, scores aren’t going away. What’s important is recognizing the embedded bias and regularly reviewing the choice of factors and weights to ensure the bias is aligned with your goals and minimizes unintended consequences.